上一篇里,我们简单的介绍了基于 Pearson 相关系数的特征选择方法,本篇介绍另一种使用更加广泛的相关系数:Spearman 秩相关系数,简称 Spearman 相关系数。Spearman 相关系数与 Pearson 相关系数、Kendall 相关系数并称统计学三大相关系数,足见其重要性。
有了 Pearson 相关系数,为什么还要用 Spearman 相关系数呢,主要是 Pearson 系数只能度量两个服从正态分布的变量之间线性相关性的强弱 (如果不熟悉可以回顾一下上一篇的介绍),而 Spearman 系数只度量单调关系,而不考虑具体数值的影响,因此 Spearman 相关系数的应用范围更广,不仅对数据分布不作任何假设,能够容忍异常值,也不需要数据的取值是等距的(例如比赛中,第 1 名和第 2 名的距离与第 2 名和第 3 名的距离是不等的),因此除非是考虑性能的影响,能用 Pearson 系数的地方都能用 Spearman 系数。
Spearman 秩相关系数的定义
Spearman 秩相关系数是一个非参数性质(与分布无关)的秩统计参数,是用来度量两个连续型变量之间单调关系强弱的相关系数,取值范围也是 $[-1,1]$。在没有重复数据的情况下,如果一个变量是另外一个变量的严格单调函数,则 Spearman 秩相关系数就是 $1$ 或 $-1$,称变量完全 Spearman 秩相关。
这里的秩相关 (Rank Correlation),又称等级相关,是将两变量的样本值按数据的大小顺序排列位次,以各要素样本值的位次代替实际数据而求得的一种统计量。排序不论从大到小还是从小到大排都无所谓,只要保证大家排序的标准一致即可。
用 $\rho_s$ 来表示 Spearman 相关系数 (用 $\rho_p$ 表示 Pearson 相关系数)。如果每个变量都没有相同的取值 (即没有相同的秩次),则 Spearman 相关系数可由下式计算:
其中,$n$ 表示数据点的个数; 表示数据点 的秩次 之差:。
如果某个变量有重复数据,则计算变量之间的 Spearman 相关系数就是计算变量数据秩次之间的 Pearson 相关系数:
其中,$r_x$ 表示变量 $\boldsymbol{x}$ 转换后的秩次。从这个定义可以看出来,Spearman 相关系数实际上就是对数据做了秩次变换后的 Pearson 相关系数。
举例说明
我们还是拿上一篇的例子来说明。首先将样本进行秩次变换,样本升序排列后的位次如图 1 所示:
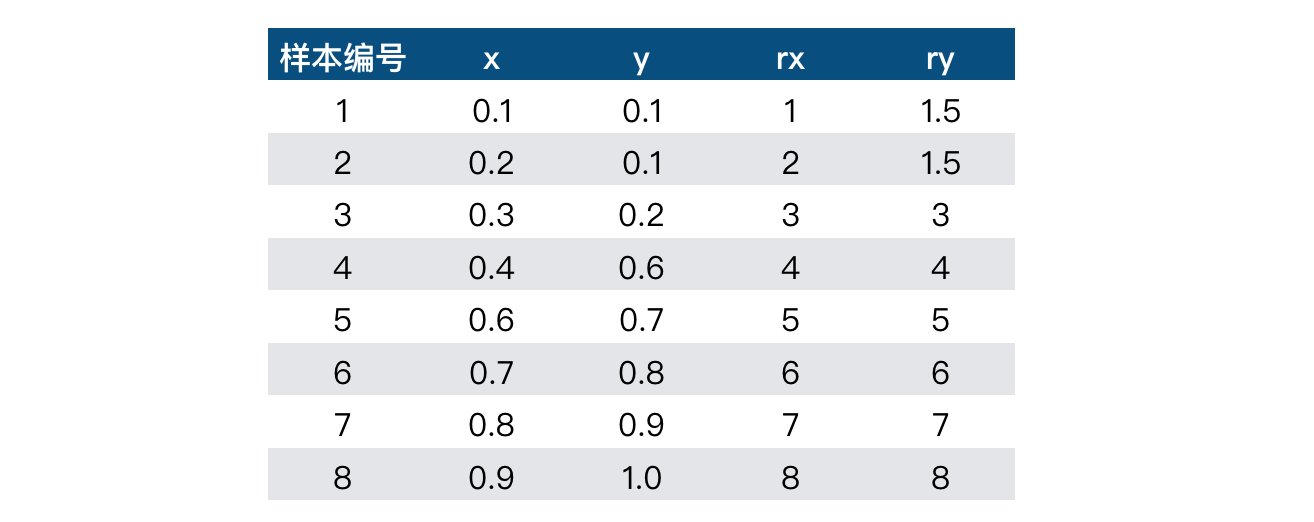
需要说明的是,这里变量 $y$ 有两个重复数据 $0.1$,在排序的时候它们的位次相同,此时可以用相同位次的数据所占的位次之和除以数据的数量 (即 $\frac{1+2}{2}=1.5$) 来作为这些重复数据的位次。
根据定义,当存在重复数据的时候,我们计算秩次 (即 $r_x$, $r_y$) 的 Pearson 相关系数 (过程省略),得到结果 $\rho_s=0.994$,几乎是单调相关了,其数值比直接计算原始数据的 Pearson 相关系数 $\rho_p=0.972$ 还要大一些。
实际上,当 Pearson 相关系数比较大的时候,Spearman 相关系数也比较大;而当 Pearson 相关系数比较小的时候,Spearman 相关系数仍然可能较大,例如变量之间是指数相关 ($y=e^x$,如图 2 所示) 时,它们的 Pearson 相关系数和 Spearman 相关系数分别是 $0.7758$ 和 $1.0$。

最后,我们看看上一篇图 3 所示的异常数据对 Spearman 相关系数的影响,引入异常点 $(0.9,-1.0)$ 后,变量 $x$, $y$ 的 Pearson 相关系数降为了 $\rho_p=-0.0556$,它们的 Spearman 相关系数也受到了较大的影响,降到了 $\rho_s=0.3234$,也就是较弱的正相关性。但是从这个例子仍然可以看出,与 Pearson 相关系数相比,Spearman 相关系数对异常值容忍度更高一些。
附示例的 python 代码:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
x=[0.1, 0.2, 0.3, 0.4, 0.6, 0.7, 0.8, 0.9]
y=[0.1, 0.1, 0.2, 0.6, 0.7, 0.8, 0.9, 1.0]
spearmanr(x,y)
(0.99402979738800479, 5.2961535156451228e-07)
rx=[1, 2, 3, 4, 5, 6, 7, 8]
ry=[1.5, 1.5, 3, 4, 5, 6, 7, 8]
pearsonr(rx,ry)
(0.99402979738800501, 5.2961535156445373e-07)
z=[0.1, 0.1, 0.2, 0.6, 0.7, 0.8, 0.9, -1.0]
spearmanr(x,z)
(0.32335909071657992, 0.43463944855085729)
z=[0.1, 0.12, 0.2, 0.6, 0.7, 0.8, 0.9, -1.0]
spearmanr(x,z)
(0.32335909071657992, 0.43463944855085729)这里,
spearmanr返回的第二个结果是 p-value,其具体含义可参考官方文档。
Take-aways
本文简单介绍了 Spearman 相关系数,主要注意点总结如下:
- Spearman 相关系数是度量两个连续型变量之间单调关系强弱的相关系数,它对数据的分布不作任何假设,能够容忍异常值,也不需要数据的取值是等距的;
- Spearman 相关系数实际上就是对数据做了秩次变换后的 Pearson 相关系数,只要能用 Pearson 相关系数的地方就能使用 Spearman 相关系数;
- Spearman 相关系数还需要对原始数据进行排序,因此计算复杂度高于 Pearson 相关系数,当数据满足 Pearson 相关系数的使用条件时,优先考虑使用 Pearson 相关系数。
这是特征选择系列文章的第二篇,其他文章可参考: