在视频推荐优化的过程中,最重要的措施莫过于 A/B 测试了。典型的 A/B 测试场景中,我们首先将流量均匀的分桶,选择部分桶使用基线算法,作为对照组(Control),选择相同数量的桶用于测试新的特性,作为实验组(Treatment)。实验过程中不断收集用户的反馈数据,用来计算核心指标(本文考虑 CTR),最后分析、评估出最好的版本。
这里分析最佳版本就需要借助假设检验的技术,例如检验某个实验组的 CTR 是否优于对照组,属于双比率检验(2 Proportion-test,用于根据两个随机样本中的数据对两个总体比率之间的差值进行推断)。由于推荐系统中样本量比较大(满足 $n\cdot(1-p)>5, n\cdot p>5$,$n$ 表示样本数,$p$ 表示 CTR),我们通常采用的是 Z 检验的技术,它是基于标准正态分布来近似推断实验组优于对照组的概率。
注意,Z 检验是大样本下的近似检验,如果需要精确检验,可以基于超几何分布来进行检验,但是数据量非常大的情况下,计算成本较高,所以一般还是使用 Z 检验技术。
具体来讲,假设对照组和实验组样本数为 $n_1,n_2$,平均 CTR 为 $\bar{p}_1,\bar{p}_2$ ,这里平均 CTR 是指我们基于实验观测到的结果,假设实际上两组的 CTR 为 $p_1,p_2$,根据中心极限定理,$p_1$ 和 $p_2$ 均趋向正态分布,且由于独立正态分布变量之和依旧是正态分布,$p_1-p_2$ 也趋向正态分布:
统计显著性
接下来,我们开始假设检验过程。首先要建立原假设(Null Hypothesis),即假设对照组不比实验组差,即 $H_0:\ p_1-p_2\ge 0$,且观测到的差异是由于随机波动引起的。我们最希望的是拒绝该假设,并接受实验组的效果显著优于对照组,即对立假设 $H_1:\ p_1<p_2$。
要拒绝零假设,我们需要根据我们观测的数据来看看 $p_1$ 是否真的不比 $p_2$ 小,如果 $p_1$ 和 $p_2$ 相差很小或者 $p_1$ 明显大于 $p_2$,则确实无法拒绝原假设;但是如果 $p_2$ 比 $p_1$ 大很多,那么我们就有把握拒绝零假设。大多少算是多呢?我们可以通过统计量 Z 来检验:
其中,$\bar{p}_1-\bar{p}_2$ 是实际观测到的差异,$\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}$ 是实际观测到的标准误差,直观来看的话,Z-score 表示的是实际差异有多少个标准误差。Z-score 与正态分布的关系如下图所示 $^{[1]}$:
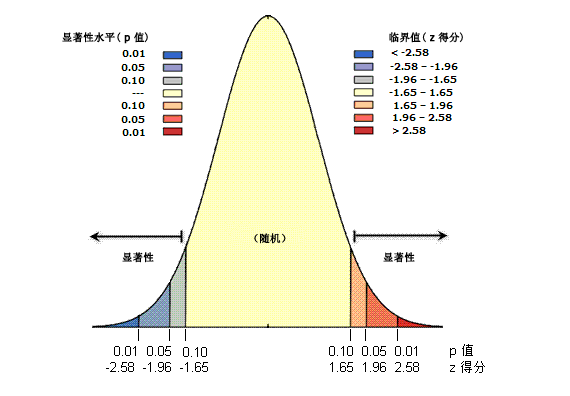
显然,Z-score 越小(负数),说明观测结果与原假设越不相符,我们越有理由拒绝原假设。那小到什么程度可以拒绝呢?这就需要人工拍一个显著水平 $\alpha$,它表示假定原假设为真时,我们却拒绝原假设的概率(即第一类错误的概率,在本文中,第一类错误是指实验组实际上不比对照组好,但是却错误的认为实验组更好)。由于错误转正一个并不好的实验组代价是很大的,我们希望 $\alpha$ 越小越好,通常取 $\alpha=0.05$。
基于 Z-score 和正态分布可以估计观测到的数据出现的概率,记为 $p$(p-value),如果 $p<\alpha$,也就是观测到数据比预期的显著水平更极端,此时可以拒绝原假设。对应到上面的图中,我们可以确定拒绝域:,或者等价的 。
总结一下上面的假设检验过程:
- 确定原假设 $H_0:\ p_1-p_2\ge 0$,对立假设 $H_1:\ p_1<p_2$;
- 确定显著水平 $\alpha=0.05$;
- 计算样本均值 $\bar{p}_1,\bar{p}_2$ 和统计量 $Z$,
- 查正态分布表得到临界值 $Z_{\alpha}=-1.96$;
- 如果 $Z\le Z_\alpha$ 成立,则拒绝原假设,并认为实验组显著优于对照组,水平为 $\alpha$;否则无法拒绝原假设。
这个过程实际上是一个单侧检验,我们还可以检验对照组与实验组是否有显著差别,即双侧检验,这里把各种情况下的假设和拒绝域都汇总帖出来。
| 双侧检验 | 左侧检验 | 右侧检验 | |
|---|---|---|---|
| 假设 | $H_0:\ p_1-p_2= 0$ $H_1:\ p_1-p_2\not =0$ |
$H_0:\ p_1-p_2\ge 0$ $H_1:\ p_1-p_2<0$ |
$H_0:\ p_1-p_2\le 0$ $H_1:\ p_1-p_2>0$ |
| 拒绝域 |
特别的,当我们原假设是 $p_1-p_2=0$ 时,也就是假设两组 CTR 没有差异,这时统计量 Z 简化为:
其中,$\bar{p}_0=\frac{c_1+c_2}{n_1+n2}$ 表示两组样本的平均 CTR。
统计功效
前面提到了,对于相同的原假设,我们可以用多种方法来检验,其中自然有优劣之分,可以用检验的功效函数来区分 $^{[2]}$。所谓检验的功效函数,简单来讲就是基于该检验之下,原假设被拒绝的概率。检验的功效越大,当原假设为假时,我们拒绝原假设的概率越大。
但如果原假设为真,我们还拒绝原假设,那不就相当于是错误的把更好的实验组给否定了吗(即第二类错误)?此时功效函数越大反而说明犯第二类错误的概率越大,说功效就不合适了。因此,一般只有原假设为假时,我们才考虑功效值。一般记某个检验发生第二类错误的概率为 $\beta$,则其功效值为 $power=1-\beta$。对于左侧检验,功效值的计算公式为:
其中,$\Phi(\cdot)$ 表示标准正态分布的累积分布函数,同时,为了简化后面的样本量分析,这里考虑 $n_1=n_2=n$,即实验组和对照组的样本量大致相同(这是符合 A/B 实验设计的要求的,如果不同,可以取 $n=\min(n_1,n_2)$)。上式具体推导过程就不详述了,右侧检验和双侧检验的功效值可以参考 $[3]$。
在选择一个检验时,我们希望它发生第一类错误和第二类错误的概率越小越好,但实际上这两者是此消彼长的,就好比置信区间和置信度的权衡一样。由于一般发生第一类错误的影响更大一些,所以我们一般控制第一类错误的概率不超过 $\alpha$,然后让功效越大越好,一般取功效值 $power=0.8$(当然,如果第二类错误的影响更大,可以控制第二类错误的概率不超过 $\beta$,再让第一类错误发生的概率越小越好)。这些概念的关系如下表所示:
| 接受 $H_0$ | 拒绝 $H_0$ | |
|---|---|---|
| $H_0$ 为真 | $\checkmark$ (置信度 $1-\alpha$) | 第一类错误,$\le\alpha$ |
| $H_0$ 为假 | 第二类错误,$\le \beta$ | $\checkmark$ (功效 $1-\beta$) |
最后,怎样在确定显著水平 $\alpha$ 的情况下,提高 Z 检验的功效值呢?增加样本量!我们可以根据功效的计算公式对所需的样本量 $n$ 进行求解(继续忽略推导过程),得到预期功效为 $1-\beta$ 的样本量为:
至此,我们已经介绍了针对 CTR 的 AB 实验如何进行 Z 检验,以及如何基于指定的显著水平 $\alpha$、统计功效 $1-\beta$ 来估计所需的样本量。文章覆盖的检验对象和类型都非常有限,在其他实验中,我们可能需要进行双侧检验,或者对人均时长、GAUC 等其他指标进行检验,就需要根据实际情况选择合适的统计量和检测法来进行检验,并估计达到指定功效的样本量。当然,如果用户量和样本量非常大,可以忽略假设检验,直接根据均值来确定最佳变体。
参考文献
[1] 什么是 z 得分?什么是 p 值?. https://desktop.arcgis.com/zh-cn/arcmap/latest/tools/spatial-statistics-toolbox/what-is-a-z-score-what-is-a-p-value.htm.
[2] 陈希孺. 概率论与数据统计. 中国科技大学出版社, 2009.
[3] 功效和样本数量. https://wenku.baidu.com/view/c807b8d48662caaedd3383c4bb4cf7ec4afeb6b3.html.