MA-GNN 论文精读

论文引用：Ma, Chen, et al. “Memory Augmented Graph Neural Networks for Sequential Recommendation.” arXiv preprint arXiv:1912.11730 (2019).

MA-GNN 是华为诺亚实验室发表在 AAAI 2020 上基于序列的长短兴趣建模和 topK 推荐的模型。文章主要解决了用户长短期兴趣如何建模、如何融和，以及如何显式建模物品的共现关系并进而用于推荐的问题。

背景与动机

在个性化推荐系统中，把握一个用户兴趣及其演变最直接和有效的途径是挖掘其行为序列。

研究表明，用户未来可能交互的物品与其历史有过交互的物品高度相关。基于这个发现，我们可以从用户行为序列中尝试提取他可能的兴趣。而用户的兴趣又可以进一步细分为长短期兴趣：从长期来看，用户的序列偏向于某个/某些类别的物品；但是在短期来看，用户的兴趣可能短暂的偏移到某个特定的类别。由于存在这种时序关系，本文说的用户行为序列是基于时间发生的先后进行排列的。

以小视频播放为例，用户长期兴趣可能是军事、战争；偶尔刷到一个钓鱼的视频（探索），感觉挺有意思的，这时候可能会希望看更多相似的视频，这时候用户的短期兴趣就变成了钓鱼；用户看了几条钓鱼的视频，可能会觉得很有趣，逐渐将其演变成长期兴趣；也可能觉得没多大意思，又想继续看军事类的视频了。推荐系统需要兼顾用户的长短期兴趣，根据用户实时反馈适当的增加或者减少基于用户短期兴趣的推荐。

文章认为，要构建一个基于用户长短兴趣推荐的模型，核心有三点：

1. 用户长期兴趣：体现在用户历史长期的行为序列中；
2. 用户短期兴趣：体现在用户最近的数个行为序列中；
3. 物品共现模式：基于用户历史序列和全局的统计分析，预测他可能还会喜欢什么；

下面详细介绍文章的解决方案。

MA-GNN (Memory Augmented Graph Neural Networks)

文章要解决的问题是：给定用户 $u$ 的行为序列，从某个时间点进行划分，将该时间点以前的序列称为历史序列并作为训练数据，用 $H^u$ 表示；将该时间点以后的序列称为目标序列并作为测试数据，用 $T^u$ 表示；训练模型来为这些用户推荐 topK 个物品，并评估这些推荐结果是否在测试数据中出现，评估指标可以使用 Recall@10 和 NDCG@10 等。这是一个典型的离线任务。

为了解决这个问题，文章设计了多个模块并进行集成，网络架构如下图所示。

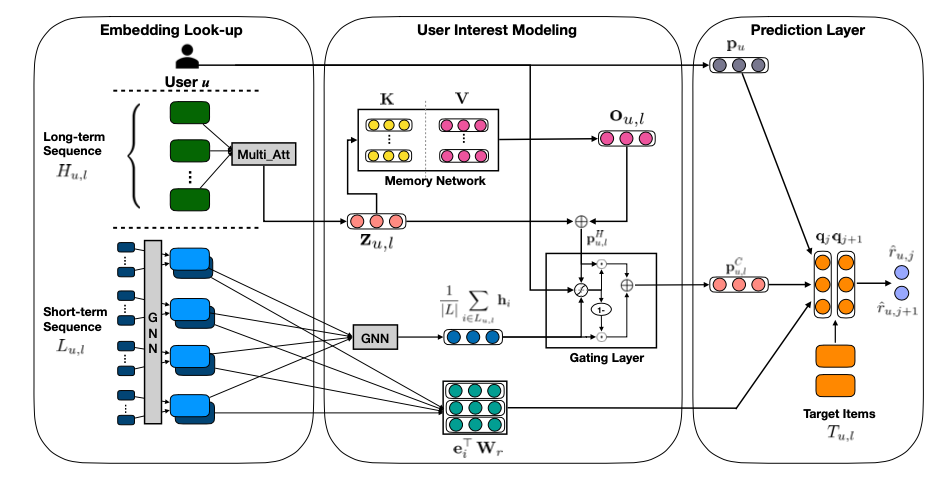
首先基于用户的历史行为，用矩阵分解等方式生成用户的稳定兴趣；基于用户短期行为，挖掘物品共现关系，并用 GNN (Graph Neural Network) 提取其短期兴趣；基于用户长期行为，用 MDAtt (Multi-dimention Attention) & MemNet (Memory Network) 提取其长期兴趣；基于 gateNet 对长短期兴趣进行融合；最后基于所有这些信息进行推荐。下面详细介绍下几个主要的模块。

用户、物品向量表示

由于物品和用户都是高维稀疏的，因此在建模之前需要获得他们在同一向量空间的低秩表示。这个表示一方面是方便联系用户和物品进行建模，另一方面也反映了用户的稳定兴趣。获得这种表示的方法有很多，文章使用了传统的矩阵分解，即对于每个用户有过交互的物品生成一条记录，用 $p_u\in \mathbb{R}^d$ 表示用户 $u$ 的向量，用 $q_i\in \mathbb{R}^d$ 表示物品 $i$ 的向量，用 $p_u^{\top}\cdot q_i$ 来预测用户是否会与该物品发生交互。

这只是获得表达的一种方式，它的主要问题是只能对有过行为的用户/物品生成 embedding，并且只能离线训练和更新。我们也可以加一些 side information，使用类似 TowerModel 的模型来生成用户 embedding，这样能够生成新用户/物品的表示。

短期兴趣建模

短期兴趣体现在用户最新的几次交互序列中，它会强烈的影响用户近期的行为。因此在建模用户短期兴趣时，文章只考虑每个用户 $u$ 最近 $t$ 个交互的子序列 $S^u $，并通过 GNN (Graph Neural Netwrok) 来聚合这个子序列的信息，从而生成用户的短期兴趣。

GNN 能够比较好的学习 local structure，并对邻居信息进行聚合。为了生成 graph，文章采用的方式是对每个用户的历史序列，依次将每个物品与其后 3 个物品分别添加无向边并设置权重为 1（如果边已经存在，就将权重加 1）。我们可以将物品进行编号，然后得到所有历史序列生成的一个连接矩阵 $A$，矩阵的每个元素 $A_{i,j}$ 表示物品 $i$ 与物品 $j$ 的边权，最后再按行对权重进行求和归一化。如下图所示：

连接矩阵 $A$ 主要是为了编码每个物品在无向图中的邻居信息。基于此，文章构建了一个两层的 GNN 来生成用户的短期兴趣，对于用户 $u$ 和他最近交互子序列 $S^u$，第一层对这个序列中每个物品 $i$ 生成一个带局部结构编码的隐向量：

$$h_i=\tanh\big(W^{(1)}\cdot[\sum_{k\in \mathcal{N_i}} e_kA_{i,k};e_i]\big), \quad \forall i\in S^u$$

这里符号 $[\cdot;\cdot]$ 表示向量拼接，即将两个 $d$ 维向量拼接成一个 $2d$ 维的向量；$e_k\in \mathbb{R}^d$ 表示物品 $k$ 的 embedding，它是网络参数的一部分，需要跟上面的 $q_k$ 区分开；$W^{(1)}\in \mathbb{R}^{d\times 2d}$ 也是 GNN 参数。

第二层将序列中所有物品的隐向量进行 avg-pooling，得到用户的短期兴趣表示 $p_u^s$：

$$p_u^s=\frac{1}{n}\sum_{i\in S^u} h_i$$

其中，$W^{(2)}\in \mathbb{R}^{d\times 2d}$ 是 GNN 参数。基于 $p_u^s$，我们就已经可以进行短期兴趣召回了。但是这个召回过于偏重最近 $t$ 个交互物品，可能会丢失用户的长期兴趣。

长期兴趣建模

为了将用户的长期兴趣考虑进来，我们需要挖掘用户 $u$ 在 $ S^u$ 之前的序列中的兴趣，记为 $L^u $，长度记为 $m$，它的矩阵表示记为 $\mathcal{L}_u$。文章为了减少存储并避免学到的长期兴趣与 $p_u $ 相似，借鉴 Transformer 的思想，对序列中物品的位置编码后，计算 MDAtt，生成用户长期行为的 query 向量，再根据共享 $K,V$ 矩阵计算加权后的用户长期兴趣。具体过程如下：

1. 对用户的行为序列 $L^u$ 进行位置编码，其中 $P(\cdot)$ 表示位置编码函数，参考 Transformer 论文 $^{[1]}$，用户历史行为序列用 $\mathcal{L}_u\in\mathbb{R}^{d\times m}$ 来表示： $$\mathcal{L}_u :=\mathcal{L}_u+P(\mathcal{L}_u)$$
2. 计算用户历史序列 $L^u$ 与其稳定兴趣 $p_u$ 的 MDAtt 权重矩阵 $\alpha_u \in \mathbb{R}^{h\times m}$，这里的 attention 使用加和的形式 $^{[1]}$，并使用 $h$ 维 attention。因此，$\alpha_u$ 的每一行表示用户历史的行为与其稳定兴趣的权重，而不同的行则表示从不同的角度得到的权重。其中，$W_a^{(1)},\ W_a^{(2)}\in\mathbb{R}^{d\times d},\ W_a^{(3)}\in\mathbb{R}^{h\times d}$ 均为 attention 相关的参数矩阵。 $$\alpha_u = \text{softmax}\Big(W_a^{(3)} \tanh\big(W_a^{(1)}\mathcal{L}_u+(W_a^{(2)}p_u)\otimes \boldsymbol{1}_m\big)\Big)$$
3. 计算每维 attetion 的加权向量，并进行 avg-pooling，得到用户历史行为的 query 向量 $z_u\in\mathbb{R}^d$： $$z_u = \text{avg}\big(\tanh(\alpha_u\cdot \mathcal{L}_u)\big)$$
4. 用 $K,V\in\mathbb{R}^{d\times n}$ 表示所有用户共享的内存网络，它们的每一列对应于一种隐式的用户兴趣，我们保存 $n$ 个隐式兴趣。我们计算 $z_u$ 与各个隐式兴趣 $K$ 向量的相关性，并作为权重计算它与 $V$ 向量的加权和，再加上残差，得到这个用户长期的综合隐式兴趣向量 $p_u^l$： $$p_u^l=z_u+\text{softmax}(z_u\cdot K)\cdot V^{\top}$$

其中，第 4 步中的 $K, V$ 矩阵就是文章所谓的内存网络 (MemNet)，它的计算跟 Self-Attention 过程很像，区别在于 Self-Attention 中，每个物品都对应 $K, V$ 矩阵的一个向量，而这里则是一个隐式的兴趣对应于一个 $K, V$ 向量。

长短期兴趣融合

前面介绍了对于用户 $u$，基于 GNN 生成最近 $t$ 个交互的表示 $p_u^s$，基于 MDAtt 和 MemNet 生成历史 $m$ 个行为的表示 $p_u^l$，接下来文章考虑如何将长短兴趣进行融合。

一个比较直观的想法是将长短期兴趣进行线性加权，比如长、短期兴趣各占 $50\%$。但是这就引入了一个很难调的超参，并且实际上用户的兴趣是动态变化的，例如有时候突然想看某些类别的视频，这个时候短期兴趣占主导，看了一会可能就没那么上头了，这时候慢慢又回归到长期兴趣来，从这个例子中我们可以看出这个超参可能是动态变化的。

因此，文章的方案是借鉴 gateNet 的思想，自动的学习这个权重如何生成。具体来讲，引入参数矩阵 $W_g^{(1)}$,$W_g^{(2)}$,$W_g^{(3)}\in\mathbb{R}^{d\times d}$ 来学习权重 $g_u$，进而算出加权融合后的兴趣表示 $p^c_u$：

$$\begin{align}g_u &= \sigma\big(W_g^{(1)}\cdot p_u^s + W_g^{(2)}\cdot p_u^l + W_g^{(3)}\cdot p_u\big)\\p_u^c &=g_u \odot p_u^s+(\boldsymbol{1}_d-g_u)\odot p_u^l\end{align}$$

物品共现模型

在预测用户是否喜欢某个物品的时候，一方面看他是否对该物品感兴趣（通过用户与物品向量表示来计算），另一方面还可以看看用户历史有过行为的物品与该物品的共现关系，即大多数据有过类似行为的用户会不会对该物品感兴趣。文章通过一个双线性映射函数来显式的对物品的共现关系进行建模，对于物品 $i,j$，它们的共现强度为：

$$e_i^{\top}\cdot W_r\cdot q_j$$

其中，$W_r\in \mathbb{R}^{d\times d}$ 是用来捕获物品在隐向量空间中的关联关系。这样，根据用户 $u$ 短期行为列表 $S^u$ 中所有物品与某个物品 $j$ 的共现强度的均值，我们就能估算从统上来讲，用户是否会对该物品感兴趣：

$$c_{u,j}=\frac{1}{n}\sum_{i\in S^u} e_i^\top\cdot W_r\cdot q_j$$

预测与训练

基于用户长短期兴趣表示以及物品间共现关系的表示，我们可以预测用户 $u$ 对某个物品 $j$ 的喜好为：

$$r_{u,j}=p_u^\top\cdot q_j + p_u^{c\top}\cdot q_j+c_{u,j}$$

在训练时，文章使用 pair-wise 的 BPR 目标，即最大化正例和负例的差距：

$$\arg\min_{P,Q,E,\Theta} \sum_u\sum_l\sum_{S^u,L^u,i,j} -\log \sigma(r_{u,i}-r_{u,j})+\lambda(\parallel P\parallel ^2+\parallel Q\parallel ^2+\parallel E\parallel^2+\parallel \Theta\parallel ^2)$$

其中，$i$ 表示正例，$j$ 表示负例，通常是随机从未观测的样本中采样，$\Theta$ 表示所有可学习的网络参数，$P,Q$ 分别表示用户/物品的向量表示 (矩阵分解生成)，$E$ 表示物品的 embedding table (网络参数)。使用反向传播和 GD 来优化该目标。

实验与讨论

文章的对比实验表示 MA-GNN 在离线效果上有一定的优化，并且研究了 head 数量和 MemNet 中隐式兴趣个数的影响，结果表明这两个值越大越好，但是 MemNet 的容量更重要一些。文章还可视化了 MemNet 的权重，发现相似的视频生成的 query 对应的 attention 权重也比较相似。

总体来看，这篇文章借鉴了 GNN、MDAtt+MemNet、gateNet、bilinearMap、MF 等思想，将序列推荐问题分解成三个小的子问题并用不同的技术去解决，最终通过端到端的训练将整个过程糅合在一起。有些地方的处理可能还是太复杂了，例如 loss 的设计，还有 MF 是否可以简化掉等，会导致生产环境中的样本组织、训练和线上推理的复杂度过高，在实际应用的时候可以根据实际情况进行调整。

参考文献

[1] Vaswani, Ashish, et al. “Attention is all you need.” Advances in neural information processing systems. 2017.
[2] Attention机制详解（一）——Seq2Seq中的Attention. https://zhuanlan.zhihu.com/p/47063917.