xDeepFM 论文精读

论文引用: Lian, Jianxun, et al. “xdeepfm: Combining explicit and implicit feature interactions for recommender systems.” Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2018.

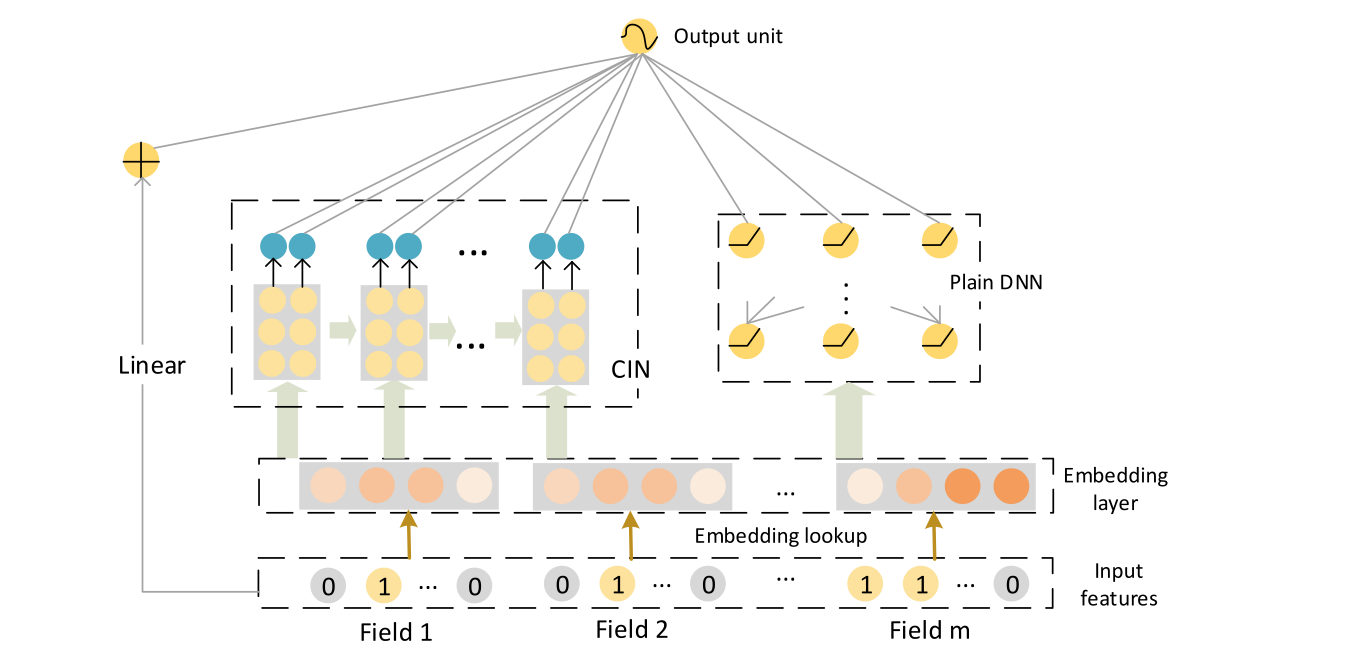
xDeepFM 是中科大和 MSRA 发表在 KDD 2018 上用于 CTR 预估的模型。这个模型充分借鉴了 DCN、FM 的思想，提出了一种新的将特征按 vector 进行交叉的结构 CIN，并且这个结构与 CNN 和 RNN 有一定的相似性。从实验来看，效果的确不错，但是工程效率实在是个难题。

背景与动机

原始特征就像是未雕琢的原石，很难直接发挥出有效的作用，在预测系统中，我们通常需要对原始特征进行一定的组合变换，来取得比较好的效果。其中，特征交叉（即将离散特征值拼成一个新的特征值）能够衡量原始特征间的交互关系，提供在组合场景下有指导性的信息，对预测效果影响也比较显著，因此自动完成并提炼这种特征变换成为了众多模型（FM、DeepFM、DCN 等）设计显式交叉结构最主要的目的。

虽然 DeepFM、FNN、PNN 等模型能够完成特征的二阶显式交叉，并且通过 MLP 来完成特征的高阶隐式交叉，但是 xDeepFM 作者认为，单纯靠 DNN 来捕获高阶交叉特征效果无法保证，既说不清楚学到的函数是什么样的，也没法证明最多能学到几阶交叉，而且 MLP 本质上还是按 bit 进行交叉，物理含义也难以解释。

DCN 模型前面也介绍过，是典型的能够提供高阶显式交叉能力，文章则证明了，DCN 的 CrossNet 结构每一层实际只能学到 embedding 层的张量积的形式。这个实际上就是看法的不同。对于第 $i+1$ 层 CrossNet，它的输出是根据 embedding 层的输入 $x_0$ 和第 $i$ 层的输出变换得到的：

$$x_{i+1} = x_0x_i^{\top}w_{i+1}+x_i$$

我们之前说 CrossNet 能够捕获所有特征两两交叉的信息，是源自它有一项 $x_0x_i^{\top}$，它的结果是个矩阵，包含两个向量每一位的乘积，然后再乘 $w_{i+1}$ 相当于是 pooling 或者信息压缩。

而文章作者是看到上式等价于 $x_{i+1}=x_0(x_i^{\top}w_{i+1})+x_i$，而括号内的是一个标量，因此我们可以根据归纳法得到：

$$\begin{align}x_1=&x_0(x_0^{\top}w_1)+x_0 = x_0(x_0^{\top}w_1+1)=\alpha^{(1)}x_0 \\x_2=&x_0(x_1^{\top}w_1)+x_1 = x_0\big((\alpha^1x_0)^{\top}w_1\big)+\alpha^{(1)}x_0=x_0\big((\alpha^{(1)}x_0)^{\top}w_1+\alpha^{(1)}\big)=\alpha^{(2)} x_0 \\\cdots \\x_{i+1}=& x_0\big((\alpha^{(i)}x_0)^{\top}w_{i+1}+\alpha^{(i)})=\alpha^{(i+1)}x_0\end{align}$$

这里的 $\alpha^i$ 是个标量，从这个表达式来看，CrossNet 的确每一层学到的是 $x_0$ 的张量积的形式。但是这并不是说 $x_k$ 与 $x_0$ 是线性相关的，只是说学到的函数形式比较受限。

因此文章设计 CIN 的核心思路有两个：一个是能够提供逐层高阶的显式特征交叉能力，另外特征交叉是按 vector 粒度进行，目标则是学到更加复杂的函数形式。

CIN 架构

文章提出 CIN 网络来完成特征显式交叉，简单来讲，它是将每一层的所有特征向量与输入层的所有特征向量进行点乘，然后用多个卷积核去做卷积，来生成特征交互的结果。具体来讲，它的交互过程如下：

记特征的 field 数量为 $m$，每个 field 特征对应的 embedding 维度都为 $d$，记 embedding 层输入为 $X^0\in \mathbb{R}^{m\times d}$，记第 $k+1$ 层 CIN 的输入（即第 $k$ 层的输出）为 $X^k\in \mathbb{R}^{h_k\times d}$。这里，$h_k$ 是我们设置的超参数，例如，我们设置 CIN 的 layers 为 $[128, 128, 128]$ 时，它实际上指定了 CIN 有三层，且第 $k$ 层的权重矩阵 $W^k\in\mathbb{R}^{h_{k-1}\times m}$ 的数量为 $128$。

假设我们已经算出来前 $k-1$ 层的输出 $X^{k-1}$，则第 $k$ 层的输出 $X^k$ 的计算过程如下：

1. 计算出 $X^{k-1}$ 与 $X^0$ 的所有 field 特征向量间的 Hadamard 积，即将第 $k-1$ 层 CIN 输出的 $h_{k-1}$ 个特征向量与 embedding 层的 $m$ 个特征向量做向量级的两两交叉，得到了 $h_{k-1}\times m$ 个交叉向量，每个向量还是 $d$ 维：

   $$Z^k_{i,j} = X^{k-1}_{i,*}\circ X^0_{j,*}, \qquad 1\le i\le h_{k-1},1\le j\le m$$

2. 在第 $k$ 层构造 $h_k$ 个可训练的权重矩阵，每个权重矩阵 $W^{k,h}$ 的维度为 $(h_{k-1},m)$，矩阵的每个元素对应了上一步中每个向量的权重，计算第 $h$ 个权重矩阵对所有向量的加权和，得到这个权重矩阵对应的加权向量 $X_{h,*}^k$，即第 $k$ 层 CIN 的输出 $X^k$ 的第 $h$ 行，每一行还是 $d$ 维：

$$X_{h,*}^k=\sum_{i=1}^{h_{k-1}} \sum_{j=1}^m W^{k,h}_{i,j} \cdot Z_{i,j}^k, \qquad 1\le h\le h_k$$

这样，我们就能够得到所有 CIN 层的输出 ${X^1,\cdots,X^n}$，并且一直保持 $X^i$ 的每一行是 $d$ 维的向量，从而保证每层都能与 $X^0$ 进行 vector 粒度的交叉。

整个 CIN 网络的输出则是将每个 $X^i\in \mathbb{R}^{h_i\times d}$ 按列进行 sum pooling，得到一个 $h_i$ 维的向量 $x_i$，然后将所有 $x_i$ 进行拼接，得到一个 $\sum_i h_i$ 维的向量。上面的过程如果用卷积的思路，可以参考下面的图示：

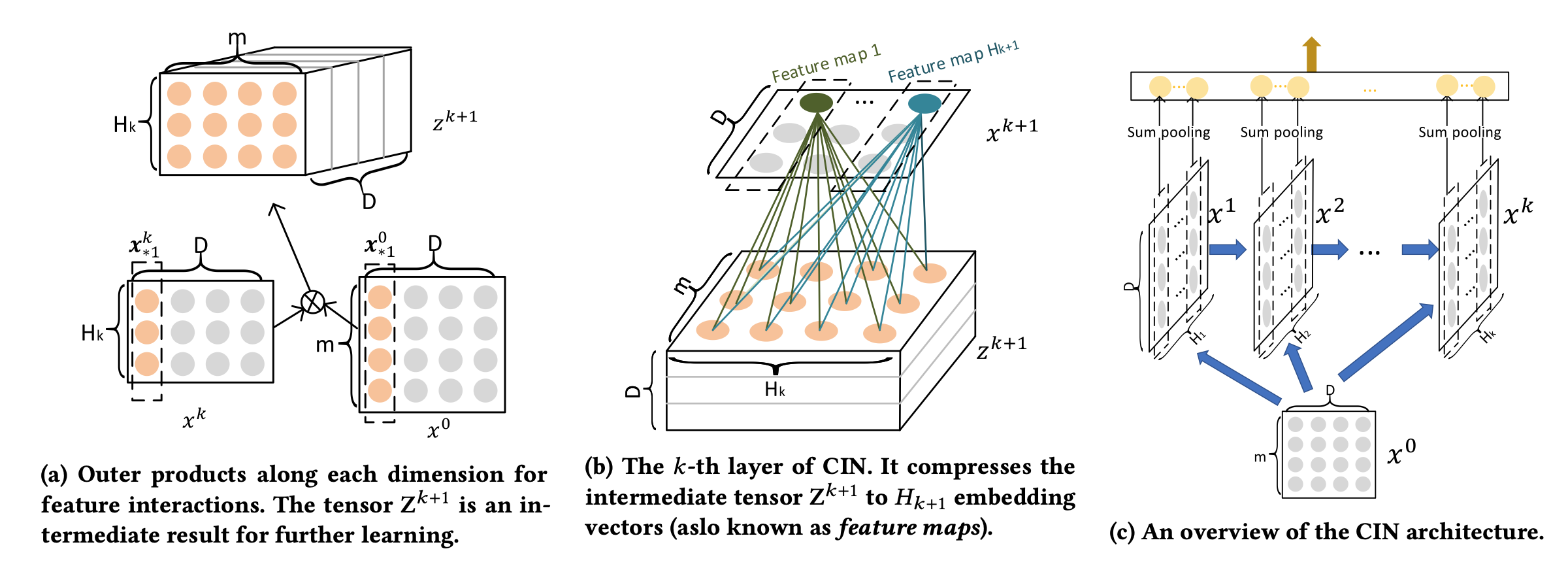
由于 CIN 层中每个权重矩阵实际上是相对独立的，每一个权重矩阵都对应了所有的特征交叉信息。因此在实现中，还可以将每个 $X^i$ 分成 $X^i_{0:h_i/2-1,*}$ 和 $X^i_{h_i/2:,*}$，前一半进行 sum pooling 后得到 $h_i/2$ 维向量直接接到输出层，后一半则作为下一层的输入。

网络分析

由于模型里可训练的参数主要是权重矩阵，根据上面的分析，CIN 的总参数量为 $\sum_k h_k\cdot h_{k-1}\cdot m$。文章也提出，如果 $h_k$ 比较大的话，可以将每个权重矩阵做 L-order decomposition，用两个小矩阵的乘积来代替，可以进一步减少参数量。

举个例子，比如 $100$ 个 field 的 $[128, 128, 128]$ 的 CIN 网络，参数量为 $3\times 128\times 128\times 100=4915200$；假设 embedding 维度为 $16$，$[128, 128, 128]$ 的 MLP 参数量为 $16\times 100\times 128+128\times 128+128\times 128=237568$；CIN 要明显多出不少。

CIN 每一层计算需要 $O(mh^2d)$ 的时间复杂度，$t$ 层的复杂度为 $O(mh^2dt)$，明显比 MLP 的 $O(mhd+h^2t)$ 大很多，实际跑下来，xDeepFM 一个 epoch 用时大概是 DeepFM 的 3 倍。因此，xDeepFM 模型无论是参数量还是训练、推理的速度，都对工程化有很高的要求。

关于 CIN 的交叉能力，从上面的网络计算过程来看，也容易知道，CIN 的交叉阶数是逐层加 1 的，这里就不展开说明了。

最后，CIN 可以与 MLP 组成并行架构，也就是文章提出的 xDeepFM，兼具显式交叉和隐式交叉的能力，如下图所示，这貌似也已经是一个通用的做法了。