论文引用: Wang, Ruoxi, et al. “Deep & cross network for ad click predictions.” Proceedings of the ADKDD’17. 2017. 1-7.
本文是 Stanford 和 Google 联合发表在 KDD 2017 workshop 上的一篇 CTR 预估模型,模型采用 Wide&Deep 架构,最大的创新点在于将 wide 层替换成 cross 层,省去了原本大量的人工特征工程的工作,由 cross 层提供显式的高阶特征组合能力,同时保持较低的参数量和计算量。
背景与动机
随着深度网络的兴起,各大厂纷纷尝试用深度网络来作为特征提取器,并取得了显著的效果。尤其是 Wide&Deep 架构的提出,让大家意识到可以在模型中同时使用 DNN 来捕获特征的复杂映射关系,使用线性模型来记忆组合特征,但是这里的线性模型中的组合特征其实还是工程师针对具体场景人工构造的。
进一步,大家考虑将 wide 层用自动特征组合的网络来替换,例如用 FM 来代替 wide 层 (DeepFM),能够提供了二阶的自动特征组合能力。本文则更进一步,设计出 cross 网络来代替 wide 层,能够提供任意高阶的特征组合能力 (与 cross 层数相同),同时保持很低的计算和存储开销。
那有了 MLP 层为什么还需要 cross 层呢?我的理解是,MLP 层更擅长的是进行特征复杂的非线性变换,这些非线性变换通常是隐式的、对于乘性的特征组合捕获能力不强,而人基于对业务的深入理解能够显式构造一些十分有效的组合特征,如果让 MLP 层去学,可能需要比较大的参数规模才能学到。这也是 Wide&Deep 为什么还需要保留 wide 层的原因。而 cross 层则设计为显式的进行特征组合,能够保证每一层都保留上一层的组合信息,并增加一阶组合,因此可以认为这两个结构是互补的。
当然,这里的 cross 层由于参数数量的限制,容量有限,我们仍然可以在 DCN 的基础上增加 wide 层来强化对部分人工特征的记忆,或者将 cross 层作为一个子网嵌入到其他排序网络中去,作为高阶特征提取器。
DCN 网络架构
前面提到了,DCN 的主要创新点在于设计了 cross 层来做特征的显式组合,同时只使用很少的参数。乍一看感觉有点神奇,如果要学习 $n$ 个特征的 $k$ 阶组合,按道理讲我们需要 $C_n^k$ 个参数 ($O(d^n)$),那怎么进行参数的压缩呢?先可以回顾一下 FM,它本质上是学习了每个特征的隐向量,然后用两个特征隐向量的内积来代替这两个特征组合的系数,这样能够共享统计强度,并减少参数量。DCN 的 cross 层则更进一步,它每一层的设计如下:
即第 $l+1$ 层的输入与第 $l$ 层的输入和原始的特征输入有关。再具体点来说,式 $(1)$ 右边的第一项是原始特征与 $l$ 阶特征的笛卡尔积,再与一个权重向量相乘。简单用归纳法可以看出,从表达式上来讲,$\boldsymbol{x}_0 \boldsymbol{x}_l$ 是能够包含所有 $l+1$ 阶的特征组合,这一项再乘以一个权重向量,相当于对特征组合的信息做了 weighted sum pooling,或者换句话说,$\boldsymbol{x}_0 \boldsymbol{x}_l^{\top}$ 的每一列 $i$ 共享同一个参数 $\boldsymbol{w}_l^{(i)}$;式 $(1)$ 最后再加上原始特征输入实际上是类似于残差网络的结构,主要是帮助模型训练。关于式 $(1)$ 文章还提供了一个可视化的图片方便理解,如下所示:
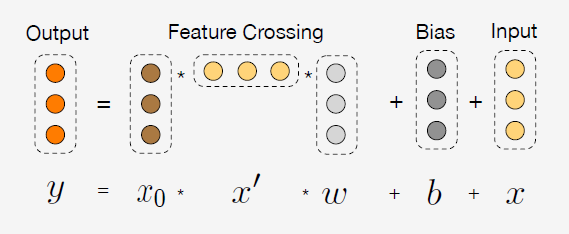
到这里我们可以简单的分析一下这个 cross 层有以下特点:
- 它的显式特征组合是通过输入与每一层进行笛卡尔积来获得,但是在保存的时候,进行了 pooling,极大的降低了存储的开销;
- 它每层的权重实际上是一个 $d$ 维的向量 (而非两层全连接网络的 的张量),因此参数规模控制在 $O(md)$ 的级别,其中 $m$ 是 cross 网络的层数,$d$ 是初始特征维度;
- 实际计算的时候,可以根据交换律先计算 $\boldsymbol{x_0} (\boldsymbol{x}_l^{\top}\boldsymbol{w})$ 中括号内的部分,将乘法次数降到 $O(d)$ 次,从而整个 cross 网络的推理复杂度也降到了 $O(md)$。
- cross 网络不存在非线性的变换,并且由于权重的连乘,在训练的时候存在梯度消失或者爆炸的风险。
我们可以将 cross 层作为一个子结构加入到其他网络中去,例如 DCN 就可以看成是普通的 MLP + cross 的架构,其中,MLP 部分主要来做特征的非线性变换,一般就是几层全连接的隐含层,使用 relu 进行激活。整体的架构如下:

在特征处理时,连续特征做归一化,离散特征先查 embedding,拼接在一起作为原始输入 $\boldsymbol{x}_0$,并分别输入到 cross 层和 MLP 层,将两个结构的输出拼接后,经过一个 LR 输出预测结果,训练的时候使用带 L2 范数的 logloss 作为 Cost Function,用 Adam 之类的优化算法求解。
对于模型训练,文章还分享了一些小技巧:
- MLP 层使用了 batch normalization,并设置梯度截断值为 100;
- 使用 early stop 来进行正则化,相对于 L2 正则和 dropout 更有效;感觉 DCN 的确比较容易过拟合,我在测试时发现,当数据量比较大,并且将模型的参数规模调整到一个合适的量级,一个 epoch 基本已经达到最优了,继续训练可能就会导致测试 AUC 下降;
- $d$ 维类别特征的 embedding size 设置参考计算式:$6\times d^{\frac{1}{4}}$;但是感觉在我们的场景里还是太大了,个人倾向于设置成 $\log$ 的函数。在资源允许的情况下,embedding size 设置大一点对测试 AUC 是有正向帮助的,但是也增加了过拟合的风险;
实验与讨论
文章主要在 criteo 数据集上进行了一些对比实验,除了证明 DCN 比 benchmark 都好很多以外,还重点强调了 DCN 在同等参数量下能够达到更低的误差、在同等误差的情况下能够使用更少的参数。另外,还单独测试了增加 cross 结构的确能够大幅的降低模型的误差。
文章比较的时候,LR、FM 等模型使用的特征与 DCN 实际上是有差别的,做了更多的特征工程。为了测试模型本身的效果,我在我们业务的数据集上也跟一些常见模型对比测试了一下,离线效果确实还不错,而且即使只用 cross 层,也能超过 FFM 的效果。
我也单独测试了 DCN 各个子结构的性能,经过若干贪心调优后,以 LR 作为基线 (即将 DCN 的 MLP 层和 cross 层的输入 $\boldsymbol{x_0}$ 直接送到 LR 层),只使用 cross 层的测试 AUC 提升了 $4.5\%$,只使用 MLP 层的测试 AUC 提升了 $5.5\%$,而两者都用的测试 AUC 提升了 $6.3\%$。只使用 cross 层效果不如只使用 MLP 层的主要原因是参数数量少了很多,即使是 10 层的 cross 层参数量也就相当于一个只含有 20 个神经元的单层全连接 MLP。如果设定两者的参数量相同的情况下,在我们的数据集上,只使用 cross 层能够比只使用 MLP 层高出 $1‰$。但是 cross 层想要把参数量提上来其实很困难,在测试中,cross 层达到 20 层的时候,训练的时长比 4 层增加 $200\%$,并且 loss 在某个 batch 以后突然爆炸(不影响 AUC 评估),因此感觉 cross 层还是只能作为一个辅助的子结构使用。一个可以尝试的方法是同时使用 2 ~ 4 层的 cross 层 (5 层相对于 4 层的收益已经很少了),在顶层进行 concat,最后送到 LR 中去。