从 SimRank 到 SimRank++

上一篇博客《SimRank与视频相似度计算》介绍了 SimRank$^{[1]}$ 及其在视频推荐中的应用，这一篇再谈谈 SimRank++。顾名思义，SimRank++ 是在 SimRank 的基础上做了一些优化，在文献 [2] 中提出时是为了解决搜索词改写的问题，本质上也就是计算搜索词的相似度。作者发现，当需要考虑二部图的边权信息时，原始的 SimRank 模型难以评估物品间相似度的可信度，这篇博客从视频推荐的角度来阐释作者的优化点。

从用户到用户群

由于我们影片的观众量级在千万级，而影片的数量在十万级，因此使用 SimRank 模型来计算视频相似度时，最大的计算和存储瓶颈在于用户相似矩阵、用户-视频转移矩阵及视频-用户转移矩阵。但是从使用场景上来讲，我们在这里实际上并不需要度量用户之间的相似度（尽管它们可以用来做用户协同推荐），用户仅仅是用来传递视频间的相似度。因此，为了减少计算和存储的开销，我们可以对用户进行聚类，使用用户组来代替用户完成视频相似度的传递。

基于这个想法，我们可以使用各种聚类的方法：按用户性别、年龄、地域等；我是直接基于历史行为进行用户聚类。具体的做法是基于用户最近 $N$ 天的播放、收藏、分享等行为生成用户的表征向量（可以用 AutoEncoder、PCA 等方法），然后基于表征向量执行 KMeans（直接 KMeans 可能跑不出来），这里的用户群数量需要根据实际场景调试，我们希望类内最大距离越小越好。然后再将用户的行为聚合到用户组，例如有效播放次数累加、总播放时长的累加、总播放占比的累加、平均 CTR 等。这样我们就从用户-视频二部图切换到了用户组-视频二部图，整个网络的规模降低了 2 个数量级。

SimRank++ 的优化

我们将用户聚成了用户组，丢失了大量的网络信息，虽然用户组作为网络中的一个节点，我们看不出它的出边是来自哪些用户，但是好在我们保留了这个组里有多少用户看了某个视频。而由于这一组用户又是相似的，因此我们期望通过充分利用边权来最小化网络信息的丢失。

SimRank++ 正好满足我们的需求，它在 SimRank 的基础上增加了两项优化：

1. 两个节点共同节点越多，则这两个节点相似度的可信度越高

这一条很容易理解，如果很多人同时看了两部视频，那这两部视频的相似度也就越可信（注意，共同观看越多并不意味着相似度越高）。例如下图所示，视频 $v_1,v_2$ 与 $v_3,v_4$ 相比同时被更多的用户组同时观看，因此 $v_1,v_2$ 根据 SimRank 模型算出来的相似度应该比 $v_3,v_4$ 的相似度更可信。

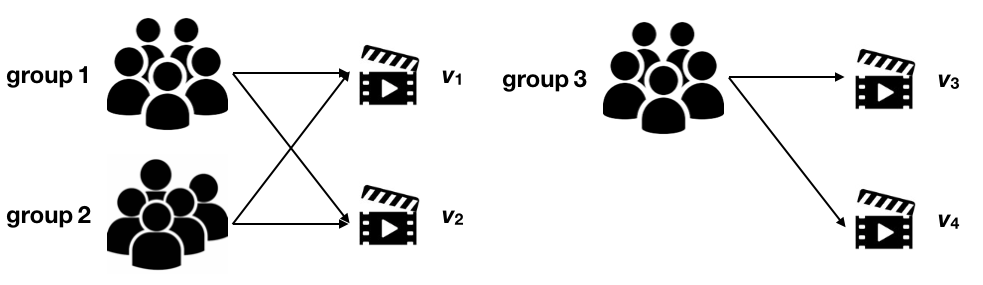
我们用 $E(i,j)$ 来表示节点 $i,j$ 相似度的可信度，论文 [2] 中推荐使用 $Ev(v_i,v_j)=\sum{k=1}^{|I(v_i)\cap I(v_j)|} \frac{1}{2^k}$ 或者 $E_v(v_i,v_j)=1-e^{|I(v_i)\cap I(v_j)|}$ 来评估该权重（用户侧的同理），则：

$\begin{cases} s(u,u')=c_1\cdot E_u(u,u')\cdot \sum_{i\in O(u)}\sum_{j\in O(u')}W_{uv}(u,i)\cdot W_{uv}(u',j)\cdot s(i, j) \\ s(v,v')=c_2\cdot E_v(v,v')\cdot \sum_{i\in I(v)}\sum_{j\in I(v')}W_{vu}(v,i)\cdot W_{vu}(v',j)\cdot s(i, j) \end{cases} \qquad (1)$

2. 节点边权越大、差异越小，则它的邻居节点相似度的权重越高

如下图所示，我们用用户播放数来表示边权（如上所述，并非只有这一种权重表示方法）。不考虑边权时，$s(v_1,v_2)$ 和 $s(v_3,v_4)$ 完全相同。但是实际上，由于用户组 1 中有 100 个人看了 $v_1$ 和 $v_2$，可以认为用户组 1 中很多人都同时喜欢 $v_1,v_2$；而用户组 2 中有 100 个人看了 $v_3$，但只有 1 个人看了 $v_4$，因此 $v_3$ 和 $v_4$ 显然相似度应该比 $v_1,v_2$ 的低。

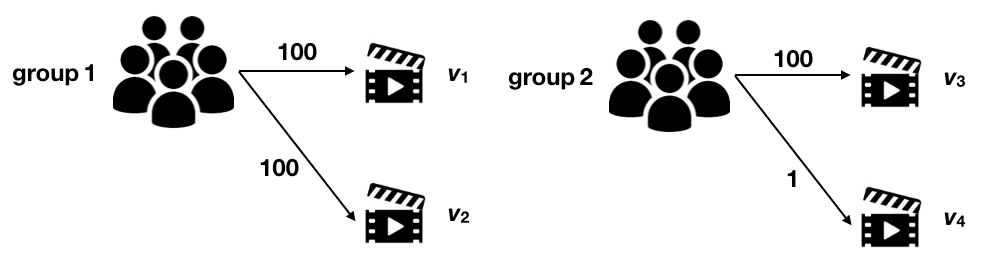
我们用新的权重 $P(i,j)$ 来表示节点 $i,j$ 的相似度传导权重，则：

$P(i,j)=e^{-var(j)}\frac{w(i,j)}{\sum_{k\in N(i)}w(i,k)}\quad (2)$

其中，$e^{-var(i)}$ 用来度量节点 $i$ 的边权差异，边权差异越大，该系数越小；$\frac{w(i,j)}{\sum_{k\in N(i)}w(i,k)}$ 则是用来计算归一化的权重。

SimRank++ 模型的矩阵描述

基于式 (1) 和式 (2)，我们可以写出 SimRank++ 的矩阵描述：

$\begin{cases} S_u^{k+1} = c_1\cdot E_u\circ P_{vu}^T\cdot S_v^k \cdot P_{vu} + (I - diag(c_1\cdot E_u\circ P_{vu}^T\cdot S_v^k \cdot P_{vu})) \\ S_v^{k+1} = c_2\cdot E_v\circ P_{uv}^T\cdot S_u^k \cdot P_{uv} + (I-diag(c_2\cdot E_v\circ P_{uv}^T\cdot S_u^k \cdot P_{uv})) \end{cases}\quad (3)$

其中，

$\begin{cases} E_u(u,u')=1-e^{-|O(u)\cap O(u')|}\\ E_v(v,v')=1-e^{-|I(v)\cap I(v')|} \end{cases}\quad (4)$ $\begin{cases} P_{uv}(u,v)=e^{-var(v)}\frac{w(u,v)}{\sum_{i\in O(u)}w(u,i)} \\ P_{vu}(v,u)=e^{-var(u)}\frac{w(v,u)}{\sum_{i\in I(v)}w(v,i)} \end{cases} \qquad(5)$

但是使用数据进行验证时，发现该模型对用户聚类的效果和权重的设置十分敏感，这两项没调好的话，很容易导致算出来的视频相似列表趋同或者有其他的问题。具体来说，用户聚类的原则是类内用户的行为越相似越好；权重的话则没有很明显的规律，需要根据业务场景来尝试了。

发散讨论：扩散算法

前几天跟其他同学交流的时候，有人提过之前做过用热传导算法来算用户的个性化推荐结果，据说效果也很不错。这里顺便扒一扒热传导算法和 SimRank 算法的区别和联系。

首先，它们都属于扩散算法，都是基于对物理世界现象的观察和模拟。典型的扩散有两类：一类是物质或者能量的扩散，满足守恒律，常称作为物质扩散，最终稳定下来后，总量是不变的；另一类是热的扩散，一般由一个或多个恒温热源驱动，不满足守恒律，常被称作为热传导。SimRank 是属于热传导（物品与自己的相似度恒定为 1）。

相比而言，物质扩散倾向于推荐比较流行的物品，而热传导倾向于推荐比较冷门的物品。更详细的讨论可以参考文献 [3]。

参考文献

[1] Jeh, G., & Widom, J. (2002, July). SimRank: a measure of structural-context similarity. In Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 538-543). ACM.

[2] Antonellis, I., Molina, H. G., & Chang, C. C. (2008). Simrank++: query rewriting through link analysis of the click graph. Proceedings of the VLDB Endowment, 1(1), 408-421.

[3] 推荐算法整理 — 扩散算法. https://www.zybuluo.com/chanvee/note/21053.