一、应用背景
最近需要对视频的相关推荐进行一些优化。之前尝试过 TagSim、AutoEncoder 和 Word2Vec 等方法,无非是基于元数据相似或基于协同相似的思路。但是在实际应用的时候,由于媒资传过来的信息未必是非常准确的,因此基于元数据相似的方法在数据基础上可能就存在一定的不确定性,因此常常会推出来一些虽然实际上很符合算法预期,但是看起来很奇怪的结果。而基于协同相似的推荐,由于需要比较多的行为数据来估计视频之间的相似度,又往往只能覆盖少量的视频。在应用中,我们往往使用的是两者的混合,但是由于混合比较简单粗暴,仍然有很多 VOC 问题。
因此,团队迫切的需要一种能够提升相关推荐效果的模型。而这种相关又是有强业务语义的,需要能够支持灵活的定制,因此在短时间内先不考虑深度网络(可解释性太差)。在调研中,发现有基于热传导的算法,感觉好像挺符合直观感觉,用了协同数据,同时也支持元数据。但是再顺着这个思路往下找的时候,发现 SimRank 是一种十分成熟且常用于相关推荐的模型,粗看了一下,感觉很符合我们的业务诉求,就迫不及待尝试了一下。
二、SimRank 基本模型
2.1 核心思想
由于 SimRank 提出的时间比较早,网上的材料很多,而且大多长的也差不多,可以参考文献 [1, 2] ,这里只简单的搬个砖。
文献 [1] 最早提出 SimRank 模型,核心的思想是 “two objects are similar if they are related to similar objects“(这跟 PageRank 的思路完全一致,只是 PageRank 是用来评估每个链接的重要性,而 SimRank 是用来评估每两个物品间的相似度)。 SimRank 既支持计算所有节点对之间的相似度(如输入数据为文章引用记录),也支持计算二部图中每一部分节点间的相似度(如输入数据为用户行为记录)。由于我们是做视频推荐,主要用的是用户行为数据,因此这里只介绍基于二部图的模型。
举个简单的例子:如下图所示,用户 $u_1$ 观看了视频 $v_1,v_2,v_3$;用户 $u_2$ 观看了视频 $v_2,v_3,v_4$,则可以用二部图来表示这种观影关系(二部图是因为用户 $u_1,u_2$ 之间无联系,且视频 $v_1,v_2,v_3,v_4$ 间无联系,只有用户-视频间存在有向边):
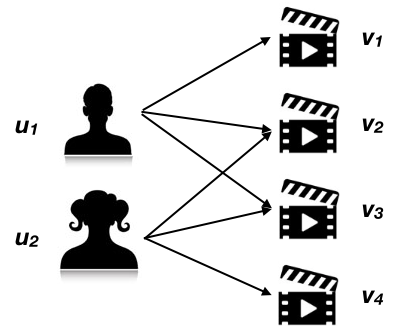
为了评估视频 $v_1,v_4$ 之间的相似度,需要看看哪些人看了 $v_1,v_4$ ,以及这些用户的相似度。这是一个典型的递归逻辑,递归的起点在于:每个节点(包括这里的用户/视频)与自己的相似度为 1;没有关联的节点间相似度为 0(一种情况是这两个节点没有与其他节点的联系,还有一种情况是在迭代的初始状态时,所有节点对间的相似度为 0)。值得注意的是,如果用 ItemCF 算法来计算 $v_1,v_4$ 的相似度,由于它们没有共同观看的用户,相似度为 0,具体对比可以参考我之前的博客:可能是最好懂的ItemCF解释了。
2.2 基于二部图的描述
最直观和容易理解的是基于图的描述。用数学语言来表达上面的思路:
其中,$u$ 表示用户,$v$ 表示视频,$O(u)$ 表示用户 $u$ 观看过的视频集合,$I(v)$ 表示视频的观看用户集合,$s(i,j)$ 表示两个节点的相似度,$c_i$ 为常数系数。式 (1) 中累加相似度的部分不是很好理解,实际上就是对两个节点所有关联的节点进行两两组合计算相似度之和。$c_1, c_2$ 可以理解成相似度的传导率,传导率越大,受到相邻节点影响也就越大,每轮迭代相似度的传播也就越快,表现为迭代若干轮后,节点间的相似度越高(文献 [1] 中建议的是0.8)。如果使用随机游走的方法,则传导率越大,下一个状态转移到相邻节点的概率越大,即下一个状态保持原来节点概率越小。
在实现模型的时候,可以直接在图上按公式 (1) 进行计算,但是需要注意缓存中间结果$^{[3]}$,否则存在很多重复计算,实测中,不做什么优化的话,超过 $10000\times10000$ 的二部图单机基本就几个小时都算不出来了。
2.3 基于矩阵的描述
另外一种等价的描述是将图转化成矩阵,比如原来的二部图是 $G = (U, V, E)$,即共 $n_u + n_v$ 个节点,可以转化成 $(n_u + n_v) \times (n_u + n_v)$ 的状态转移矩阵 $W$。根据公式 (1) 的描述,图中的每一条边对应于转移矩阵的一个元素(这里实现的时候用户和视频一般是分开连续编号的),从而可以设置转移矩阵为:
转移矩阵中其他元素为 0。而根据定义,相似度矩阵 $S$ 中对角线始终为 1,其他元素初始化为 0。则基于矩阵的迭代过程可以用下式来表达:
其中,矩阵 $C$ 的对角线元素为 或 ,如果 ,那 $C$ 可以直接用系数 $c$ 来代替。公式 (2) 的前一部分就是公式 (1) 的矩阵描述,后一部分实际上是为了设置每轮迭代时,相似矩阵的对角线为 1,即 。
注意到,在二部图的情况下,用户-视频的相似度必然是 0,同时,用户-用户 / 视频-视频的转移矩阵也必然是 0。因此相似矩阵和转移矩阵可以简单的拆成用户-用户相似矩阵 、视频-视频 相似矩阵以及用户-视频转移矩阵 、视频-用户转移矩阵 $W_{vu}$,并做分块乘法。简单的推导一下:
仔细品味一下这个公式,能更直观的了解相似度的传递过程。因此,迭代计算公式为:
2.4 扩展用户/视频属性
以上描述了经典的基于二部图的 SimRank 算法,但是其实我们可以将视频的元数据/用户的属性数据作为辅助节点加入到图中来,并添加视频元数据$\rightarrow$视频和用户画像$\rightarrow$用户的单向边(表示用户/视频的相似度不会反向传播给画像/元数据),同时初始化不同维度的视频元数据/用户画像的相似度,以达到运营干预的目的。具体的分块乘法就不推导了,跟 2.3 节差不多,这里只举一个例子:
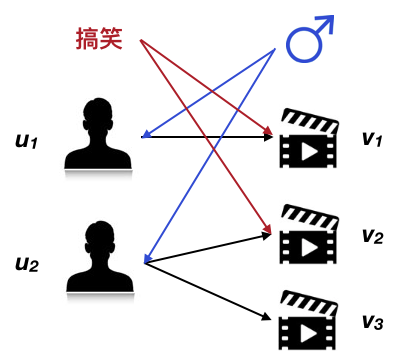
上图中,本来 $u_1,u_2$ 之间是没有边相连的,因此相似度为 0,但是由于他们同属男性,因此由男性这个画像向这两个用户传播了一定的相似度;同样的,本来 $v_1,v_2$ 之间的相似度也为 0,但是由于它们都是搞笑的视频,因此搞笑这个元数据也向它们传播了一定的相似度。加入用户维度和视频维度的辅助节点以后,有助于解决由于行为较少而无法准确评估相似度的情况。
三、模型实现与优化讨论
我在 spark 2 和在 python 中分别实现了上述过程,使用图遍历的方式优点是代码简单,但是对于大规模的图优化比较麻烦,速度很慢;使用矩阵计算的时候,主要的问题又在于矩阵的优化计算。下面简单讲下一些可行的优化思路。
a. 基于 spark 的精确计算
如果使用 mllib 的 BlockMatrix 来计算,会强制将稀疏矩阵转成稠密矩阵来计算,因此开销比实际需要的大很多,因此一定要使用公式 (3) 来替代公式 (2)。但是即使这样,也不能从根本上解决问题,根本上是需要自己实现一套高效的分布式稀疏矩阵的计算方法,网上有一些开源项目可参考。
b. 基于 python 的精确计算
使用 python 进行计算时,由于相似度的精度要求不高,因此使用 np.float16 就足够了,并且每轮迭代完,要将小于一定阈值的相似项置 0(如果只需要计算 topN相似的话,每轮可以只保留系数最大的 topN 项)。另外,构建矩阵用 csr_matrix 比较方便,计算的时候还是得用 li_matrix。
c. 迭代近似
由于我们只需要算视频的相似度,有一种解决上面问题的思路是将用户随机分成若干份,用这些用户的数据来计算视频的相似矩阵,然后将这些相似矩阵加起来求平均,但是效果不是很好。
d. 矩阵分析
针对矩阵运算,可以预先分析矩阵的特点,然后再采用一定的手段来减少总计算量。这里涉及一些矩阵分解的优化方法,以后有机会再仔细研究研究。
参考文献
[1] Jeh, G., & Widom, J. (2002, July). SimRank: a measure of structural-context similarity. In Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 538-543). ACM.
[2] SimRank协同过滤推荐算法: http://www.cnblogs.com/pinard/p/6362647.html.
[3] Lizorkin, D., Velikhov, P., Grinev, M., & Turdakov, D. (2008). Accuracy estimate and optimization techniques for simrank computation. Proceedings of the VLDB Endowment, 1(1), 422-433.